Reporte # 4
Un reporte que explica en qué sentido el fenómeno que estás estudiando tiene características de un sistema caótico y qué implicaciones tiene esto en su modelado.
Un programa que contiene uno o los dos de los elementos siguientes: (a) análisis de datos reales que indica que se trata de un señal caótico (típicamente una serie de tiempo, pero podría ser otra cosa) y (b) sistema de ecuaciones u otro modelo "artificial" para el fenómeno que da lugar a cáos - ambos (a) y (b) incluyendo código fuente y alguna ilustración de lo que se obtuvo
Un programa que contiene uno o los dos de los elementos siguientes: (a) análisis de datos reales que indica que se trata de un señal caótico (típicamente una serie de tiempo, pero podría ser otra cosa) y (b) sistema de ecuaciones u otro modelo "artificial" para el fenómeno que da lugar a cáos - ambos (a) y (b) incluyendo código fuente y alguna ilustración de lo que se obtuvo
Comenzando con el Reporte
Los sistemas dinámicos se pueden clasificar en tres:
- Estables
- Inestables
- Caóticos
En un sistema caótico manifiesta o presenta los dos comportamientos.
Haciendo mas extensa la definición.
Un sistema caótico se caracteriza por el hecho de que una pequeña variación en las condiciones iniciales puede llegar a hacerlo impredecible en el curso del tiempo; por ejemplo: perder el metro nos lleva, en principio, a una situación predecible que se puede traducir en un retraso de unos diez minutos de aquello que queríamos hacer.
Es imposible saber las variaciones y es por eso que no podemos conocer con exactitud los acontecimientos futuros. Como no se puede saber los valores de las variables que afectan, se dice que es un sistema caótico en donde cualquier evento por insignificante que sea tiene el poder de cambiar el sistema por completo.
Lo que mas representa a los sistemas caóticos son los Fractales
Fractales
Son objetos semigeométrico cuya estructura básica, fragmentada o irregular, se repite a diferentes escalas.
El término fractal proviene del latín fractus: quebrar.
Fue introducido en 1970 por Benoit Mandelbrot, en su libro “La geometría Fractal de la Naturaleza”. Pero los fractales en sí han existido por mucho tiempo.
La Geometría Fractal es un lenguaje, más que un conjunto de figuras. Este lenguaje utiliza ciertos algoritmos iterativos, vale decir reglas y procedimientos repetitivos, que se aplican hasta conseguir una estructura límite que es el fractal resultante.
La Geometría Fractal es un lenguaje, más que un conjunto de figuras. Este lenguaje utiliza ciertos algoritmos iterativos, vale decir reglas y procedimientos repetitivos, que se aplican hasta conseguir una estructura límite que es el fractal resultante.
Un Fractal Natural es un elemento de la naturaleza que puede ser descrito mediante la geometría fractal. Las nubes, las montañas, el sistema circulatorio, las líneas costeras o los copos de nieve son fractales naturales.
Alfombra de Sierpinski
La alfombra de Sierpiński es un conjunto fractal descrito por primera vez por Wacław Sierpiński en 1916.
La alfombra de Sierpinski es una variante de un Conjunto de Cantor plano en la que el cuadrado inicial se transforma suprimiéndole el cuadrado central de lado 1/3. En cada uno de los 8 cuadrados de lado 1/3 que forman la figura restante se repite esta operación. Y así sucesivamente.

Las formulas para determinarla consisten en esto:
Como ven no se incluye el punto x/3 + 1/3, y / 3 + 1 / 3 ya que este seria el punto centro y como queremos que este blanco pues no se pone.
Código
Me base del Blog de Abraham
Para hacer el código ya que lo que el hizo tiene mucha por no decir demasiada semejanza con lo mío.
A continuación pongo el código hecho en Python para generarlo.
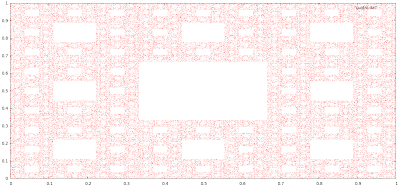
Y aquí la imagen obtenida por gnuplot.
Cabe recalcar que mientras mas iteraciones le pidas a Python mas preciso y detallado se vera la imagen (considerar que Python se tomaría un tiempo para grandes iteraciones, así que no estresarse).
Demostrando el Caos
El siguiente paso seria el jugar un poco con el, en este cambiaremos los valores de algunas ecuaciones para ver el resultado en la imagen.
Cambiando la fórmula de X en r ==1 por X = X/4
Cambiando la fórmula de Y en r ==7 por Y = X/3 + 1/3
Cambiando la fórmula de X en r == 4 por X = X/3 + 1/3
f 1 (x,y) = ( x / 3 , y / 3 )
f 2 (x,y) = ( x / 3 + 1 / 3 , y /3 )
f 3 (x,y) = ( x / 3 + 2 / 3 , y / 3 )
f 4 (x,y) = ( x / 3 , y / 3 + 1 / 3 )
f 5 (x,y) = ( x / 3 + 2 / 3 , y / 3 + 1 / 3)
f 6 (x,y) = ( x / 3 , y / 3 + 2 / 3 )
f 7 (x,y) = ( x / 3 + 1 / 3 , y / 3 + 2 / 3 )
f 8 (x,y) = ( x / 3 + 2 / 3 , y / 3 + 2 / 3 )
Como ven no se incluye el punto x/3 + 1/3, y / 3 + 1 / 3 ya que este seria el punto centro y como queremos que este blanco pues no se pone.
Código
Me base del Blog de Abraham
A continuación pongo el código hecho en Python para generarlo.
Y aquí la imagen obtenida por gnuplot.
Cabe recalcar que mientras mas iteraciones le pidas a Python mas preciso y detallado se vera la imagen (considerar que Python se tomaría un tiempo para grandes iteraciones, así que no estresarse).
50000 Iteraciones
100000 Iteraciones
Demostrando el Caos
El siguiente paso seria el jugar un poco con el, en este cambiaremos los valores de algunas ecuaciones para ver el resultado en la imagen.
Cambiando la fórmula de X en r ==1 por X = X/4
Cambiando la fórmula de Y en r ==7 por Y = X/3 + 1/3
Cambiando la fórmula de X en r == 4 por X = X/3 + 1/3
Bibliografías





Bien; puntos completos con los castigos de retraso que aplican.
ResponderEliminar